>Intro to DigiTech
An Introduction to DigiTech - How Data is Processed in Computers
Making A Start
This two-hour lesson is intended as a foundation for learning about how computers process data. This is a great starter to each cycle as it helps to explain how binary is the basis for other processes such as how a computer deals with choosing what colours to display on a screen.
I never get bored of this lesson as I alter it with every iteration. I almost want to video the lesson for other teachers to see how I have progressed as I want them to be able to take what I have done and 'make it their own'.
Understanding Decimal
I have taught this starter lesson over 100 times in the last few years. I have found that this has consistently been a fun way to get students to understand how binary numbers work.
I start by briefly visiting how we usually count in decimal. I discuss that counting is really about recognizing patterns in numbers.

As part of the explanation, I emphasise that when we run out of digits (or when we get to 9) the last digit starts again at '0' and a '1' is put in front to make the number '10'. When we get to '99', the digits start again at '00' and a '1' is put in front to make the number '100'. What other words begin with Dec? Decade, decathlon, decagon, December...

All of these words are related to 10, except December is the 12th month of the year. Or is it?
Disclaimer: Please be aware that I autoplay this video from the start to 3:14 as there are some words that are definitely not deemed appropriate for an audience of 11 or 12-year-olds!
Understanding Binary
Binary is as easy as 01, 10, 11!

I now move to how we count using binary numbers, I again emphasise that when we run out of digits (or when we get to 1) the last digit starts again at '0' and a '1' is put in front to make the number '10'. It is important to explain that the number looks like ten but we actually say 'one-zero' as it only has the value of two if we are counting in decimal. When we get to '11', the digits start again at '00' and a '1' is put in front to make the number '100'. The discussion is directed back to the pattern that the numbers are making.

The students are encouraged to recognise what patterns they can see within the numbers and the concept is reinforced using binary cards as a way to explore this further.
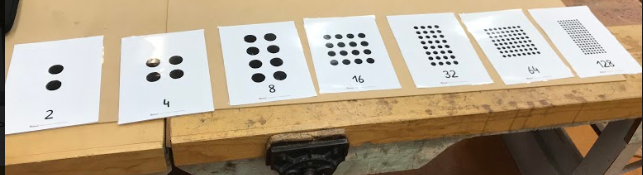
I feel that it is important to understand the concept of exponential growth and the transition from a bit to a yottabyte...


Understanding Hexadecimal
One of the things that I have added to this lesson over time is the concept of how hexadecimal numbers play a part in how a computer deals with processing all the different combinations of colours. We firstly count from zero to nine then I get my students to work out what the other six 'digits' are. They realise that we need a substitute so we use letters A to F. I then demonstrate how counting in sixteens works. Once again emphasise that when we run out of digits (or when we get to F) the last digit starts again at '0' and a '1' is put in front to make the number '10' exactly as in Binary and Decimal.

Some students in the class make the connection to what the 'name' of the six digit hexadecimal number associated with all of the colours used in graphics software.
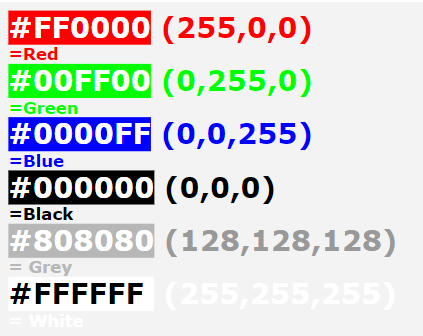
Hexadecimal numbers are used on web pages to set colours.
The colour is defined by its mix of Red, Green and Blue, each of which can be in the range:
- 00 to FF (in hexadecimal)
- 0 to 255 (in decimal)
As each of the three colours can have values above, we can work out how many colours there are in total by using this formula:

This means a screen using RGB can produce 16,777,216 different colours.
Here is an example of some colours represented in Hexadecimal and RGB values.
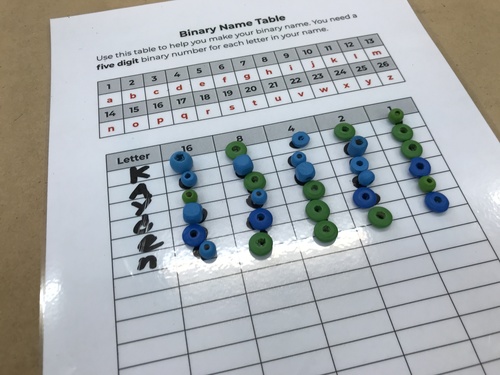
Binary Name Beads
To consolidate what we have discussed in the lesson and knowledge of the concept of binary in a fun way, the students create their own necklace, bracelet, keyring or a bag tag by writing their names in 5-bit binary. They have to decide on what bead colour will represent 0 and what colour represents a 1.



The learning that takes place in this first two-hour lesson has certainly paid off over the course of the year as the opportunities for further conversations in class over the remaining lessons will often be referenced back to the concepts learned here.
|
© Copyright 2026 Malcolm Clarke - Reflective Profile |

